【機械学習講座6】STEP３：学習ルール選定

こんにちは，shun（@datasciencemore）です！！

今回は予測モデリングのSTEP３，学習ルール選定についてやっていきます．

STEP３：学習ルール選定は，図の赤点線枠で囲った部分に該当します．

０．学習ルール選定ってなに？？
１．アルゴリズムの種類
- １．１．tree系
- １．２．linear系
２．ハイパラの種類
- ２．１．tree系
- １．２．linear系
まとめ

０．学習ルール選定ってなに？？

学習ルール選定ってなんですか？？

学習ルールはアルゴリズムとハイパラを合わせたもので，これにより学習データをどのように学習するかが決まるよ！！
学習ルールは様々考えられるんだけど，学習ルール選定とは，それらの様々な学習ルールの中から良さげな学習ルールを選定することだよ！！

さて，またまた予測モデリングと人間の学習プロセスの比較を思い出してください．

予測モデリングの学習ルール選定は，人間の学習プロセスでは，良い先生と学習計画の候補を選定することに該当していましたね．

要はアルゴリズム　＝　先生，ハイパラ　=　学習計画でその2つを合わせたものが学習ルールだと考えていただければイメージしやすいと思います．

いくら過去問や問題集が一緒でも教え方が違うと成長が全然違うことは皆様，実感としてあるのではないでしょうか？

なので，私たちはレビューが高かったり口コミがいい先生の情報を集めます．

また，ハイパラは，学習計画に該当します．

この学習計画には，問題をどのように組み合わせるか，問題をどのような順番で解いていくかなど，試験合格のためにするべきことの詳細が書かれているんだと考えてください．

もし先生が優秀でも学習計画が何もなかったり，不備があったりしたら，適切に学習できずに試験も不合格となってしまうでしょう．

また，先生があまり優秀でなくても学習計画の品質が高ければ，学習がスムーズにいくかもしれません．

このように先生と学習計画により，成績がどれくらい伸びるかが大きく異なってくることがわかると思います．

予測モデリングでも同様に，アルゴリズム，ハイパラの2つの組み合わせ方により，学習ルールが決まり，同じ学習データを使用したとしても最終的なモデルの優劣が異なってくるのです．

よって学習ルール選定では，多種多様な組み合わせが考えられる学習ルールの中から良さげな学習ルールを選定する必要があります．

どのようなアルゴリズムとハイパラがあるかは次項で詳細に説明します．

もしかしたら文献によっては，上の図の用語と異なる用語を使用しているかもしれません．
例えば，上の図では学習ルールとなっているところをモデルと呼んでいる場合もあります．
※ちなみに学習ルールは僕の造語です．アルゴリズムとハイパーパラメータを組み合わせたものについて，正式名称がないので，自分で言葉を作っちゃいました．
機械学習が理解しづらい原因の一つにこのように言葉が統一されていないということが挙げられると思います．
大事なのは言葉ではなく，どのような流れでモデリングがされていくかということです．
そのことを常に意識し，わからなくなったら図にもどって確認するようにしてくださいね！

１．アルゴリズムの種類

さっそくアルゴリズムの種類を見てみましょう．

といってもアルゴリズムをすべて紹介すると時間がいくらあっても足りませんので，超重要なアルゴリズムを厳選して紹介いたします．

こちらが厳選したアルゴリズムたちになります．

ほんとはもっとたくさんあるんですけど，まずこちらを押さえていただきたいのでかなり絞っております．

機械学習のアルゴリズムは超ざっくり分類するとtree系とlinear系に分類することができます．

さらに

tree系は，決定木，ランダムフォレスト，勾配ブースティング

linear系は，線形回帰，ニューラルネットワーク，ディープラーニング

とより細かく分類できます．

ちなみに右に行けば行くほど複雑な事象を表現することができます．

機械学習のアルゴリズムは，突き詰めるとどれも類似性をどのように表現するかということにいきつきます．
要するに機械学習のアルゴリズムは，どの説明変数同士が似ているのかということを数式で表現しているのです．
だって同じような説明変数だったら当然同じような目的変数が出るはずですもんね．
（というか，機械学習はそのような前提条件が実はあります，これも意外と説明されることは少ないですが．．．笑）

１．１．tree系

①決定木

決定木は，条件を満たすかどうかを繰り返し質問することで，類似性を徐々に高めていくアルゴリズムのことです.

目的変数について似た者同士を集めることで，似た者同士のグループに分類します．

どうやって似た者同士のグループに分類するかというと，説明変数の値よりも大きいか小さいかという質問を繰り返すことで，どんどん似た者同士のグループに近づくように分割していくのです．

言葉だけだとよくわからないと思うので，また図を見てみましょう．

こちらは，例によって健康診断データです．

今回はわかりやすいようにするため，体重を説明変数，身長を目的変数としましょう．

とある学習データがあって，これを似た者同士に分類することを考えてみましょう．

まず，どのようなデータか把握するために体重（説明変数）と身長（目的変数）の関係を可視化してみましょう．

すると，体重が60キロと70キロのところで図のように分割すると，身長が160センチ台のグループ，170センチ台のグループ，180センチ台のグループにうまく分類できそうですね．

試しに体重が60キロより小さいかどうか，70キロより小さいかどうかという質問をしてみることにしましょう．

すると右の樹形図のように学習データが分類できることがわかります．

木の一番下にご注目ください．

160センチ台グループ，170センチ台グループ，180センチ台グループときれいに分類できていることがわかります．

この木がまさに学習データの正解パターンを学習したルール（モデル）を示しています．

最後に評価データをモデルに適用して，評価データの各行（説明変数）がどのグループに該当するのかを決定してあげましょう．

この例でいうと，体重65キロなので，一番目の分岐（60より小さいか？）では，右，2番目の分岐（70より小さいか？）では，左になりますね．

なので，170センチ台グループということになります．

ちなみに予測値としては，学習データの似た者同士グループを平均した値が使用されることが多いです．

今回の場合は，160センチ台グループは，164センチ，170センチ台グループは，174センチ，180センチ台グループは，183センチということになります．

この例では，わかりやすいよう，体重60キロ，70キロを条件にしました．
実は，内部ではそれ以外にもいろいろな条件パターンを試しています．
よって木も複数できることになりますが，それらの複数の木から一番適切な木を選んでいるんですね．
この一番適切な木をモデルとしているのです．
ちなみに何をもって適切かを判断するかというと，分散，ジニ係数，エントロピーなどの指標をもとに判定しています．

②ランダムフォレスト

ランダムフォレストは，決定木を進化させたアルゴリズムです．

決定木だけでは表現できる木に限界があります．

例えば，先ほどの例で見た学習データに加えて，体重が軽いのに身長が高い人（極端に痩せている人），もしくは体重が重いのに身長が低い人（極端に太っている人）のデータが追加された時のことを考えてみましょう．

そのような場合，先ほどの例と同様の条件で考えると，体重が軽いのに身長が高い人は160センチ台のグループに，体重が重いのに身長が低い人は180センチ台のグループに分類されてしまいます．

このように極端な値（外れ値という）が紛れ込んでいると，似た者同士のグループに分類することが難しくなってしまいます．

また，決定木は，過学習を起こしやすいことも知られています．

これらの弱点を補ったアルゴリズムがランダムフォレストです．

ランダムフォレストの流れは以下のとおりです．

①学習データを色々な形に分割する．
②それぞれの分割した学習データごとに決定木を適用することで木（モデル）を作成する．
③各木の予測値を平均した数値を結果とする．

作成される木が並列なことに注目してください．

このようにすることで単一の決定木と比較し，多様性が生まれることで表現力の幅がアップするのです！

③勾配ブースティング

勾配ブースティングは，ランダムフォレストをさらに進化させたアルゴリズムです．

ランダムフォレストのさらなる改良として，予測がうまくいっているグループとうまくいっていないグループに分けて，うまくいっていないグループについてはより正解に近づけるという工夫をすることでさらなる精度向上に貢献しています．

勾配ブースティングの流れは以下のとおりです．

① 学習データを分割する．
② 分割した学習データに決定木を適用し，木（モデル）を作成する．
③ 分割した学習データにモデルを適用し，学習データの予測値を算出する．
④ 目的変数と予測値の差を取り，それを新たな目的変数とする．
⑤ ①～④を何回も繰り返す．
⑥ 評価データを⑤でできた複数の木（モデル）に適用し，算出された各木の予測値を合計する．

作成される木が直列なことに注目してください．（ランダムフォレストは木が並列でしたね）

このようにすることでランダムフォレストの多様性に加え，予測の優劣を追加しているので，ランダムフォレストよりもさらに表現力の幅がアップします！

実は勾配ブースティングは，決定木ではなくてもできます．
別に決定木でなくても，どのようなアルゴリズムでも学習データの予測値が算出できればOKです．
ただ決定木が計算コストが低く使いやすいため，勾配ブースティングといったらほぼ決定木を使用しています．
また，勾配ブースティングという名前は，決定木を分岐すべきかどうかを勾配情報を使用して決定しているためにつけられています．

１．２．linear系

①線形回帰

線形回帰は，説明変数と目的変数の関係を線形で表現するアルゴリズムのことです.

いい感じの直線の傾きと切片を見つけることで，説明変数と目的変数の関係を数式で表現します．

こちらも図を見てみましょう．

先ほどと同様，今回も体重を説明変数，身長を目的変数とします．

線形回帰は，説明変数と目的変数の関係は直線であるという前提のもと，ベストな傾きと切片を探します．

例えば，図には，赤色，緑色，灰色の3本の直線があります．

これらは，すべて傾きと切片が異なります．

どの直線が一番，説明変数（体重）と目的変数（身長）の関係を表しているかは一目瞭然です．

そう，赤色が一番データにフィットしているのがわかりますね！

こんな感じで傾きと切片の値を色々変化させて，一番データにフィットする（誤差が最小になる）傾きと切片の値を説明変数（体重）と目的変数（身長）の関係としてあげます．

正確に言うと実は線形回帰は，傾きと切片の値を色々変化させないで，一番データにフィットする傾きと切片を計算で算出します．（これを難しい言葉で言うと解析的に解くといいます．）
しかし，傾きと切片の値を色々変化させて，一番データにフィットするものを選択するという考え方は非常に応用が利き，よく使用されるので先ほどのような説明をしました．
細かいところなのであまり気にしなくてOKです笑

ちなみに説明変数が1つの場合は，単回帰，2つ以上の場合は重回帰といいます．

重回帰の場合は，直線ではなく，平面や超平面になりますが，イメージとしては単回帰の直線をイメージすれば問題ないです．

線形回帰の分類版をロジスティック回帰とよびます．
分類なのに，ロジスティック回帰と回帰となっているのが謎ですね笑
これはロジスティック回帰を英訳するとLogistic regressionなのですが，直訳していることが原因です笑
ややこしいですが，難しいことは考えずに先に進みましょう．

②ニューラルネットワーク

tree系では，決定木を進化させたアルゴリズムがランダムフォレストでした．

決定木だと表現力が乏しいので，木の多様性を増やすことにより表現力をアップさせたのでした．

さて，tree系の線形回帰でも決定木と同様の表現力が乏しいという問題があります．

それを解消したのがニューラルネットワークというアルゴリズムです！！

線形回帰の弱点は，直線的な関係しか表せないことです．

これは，体重50キロでも体重100キロでも体重1キロあたりの身長の増加率（1キロ増えるたとき，身長がどれだけ増えるか　＝　傾き）が同じということを示しています．

しかし，よく考えると体重100キロあたりの人は肥満の可能性が高いです．

肥満の人とそうでない人では，体重1キロあたりの身長の増加率は違うはずなので，線形回帰ではうまく表現できないですよね

このように，現実の現象は線形回帰だけで表現することは難しいのです．

そこでどうするかというと，右下のように重みと活性化関数を使用して，線形変換に加え，非線形変換も合わせることで表現力アップを実現させるのです！

これにより，線形だけだと赤線のような関係しか表現できなかったのが，オレンジ色のような関係も表現できるようになるのです！

③ディープラーニング

ディープラーニングは，ニューラルネットワークの進化版です！

基本は，ニューラルネットワークの中間層をさらに深くすることにより重みを増やすことで表現力をさらにアップさせています．

ディープラーニングの難しいところは，ただ中間層を深くすれば精度が上がるというわけではないというところです．

中間層を深くすることに加え，様々な工夫（ドロップアウトや転移学習など）をすることでニューラルネットワークを超える表現力を実現させるのです！

ディープラーニングは奥がとても深いため，本講座ではこれ以上立ち入りません笑

ニューラルネットワークの進化版ということだけ覚えてください！

２．ハイパラの種類

アルゴリズムは，単体だと動作しません．

アルゴリズムに対して，ハイパラを設定してあげることで初めて正解パターンの学習ルール（どのように正解パターンを学習するか）が定まります．

ここでは，各アルゴリズムに対し，どのようなハイパラがあるのかを説明いたします．

ハイパラは，利用するパッケージによって微妙に違う場合があります．
今回は，Rのtidymodelsというパッケージのハイパラを紹介します．
別のパッケージを使用する際は，それに合わせてください．

２．１．tree系

tree系はハイパラにより，木構造の複雑さを表現します．

木は分岐すればするほど，より表現力が増しますが，その分，過学習を起こしやすくなります．

①決定木

全部で３つのハイパラがあります．

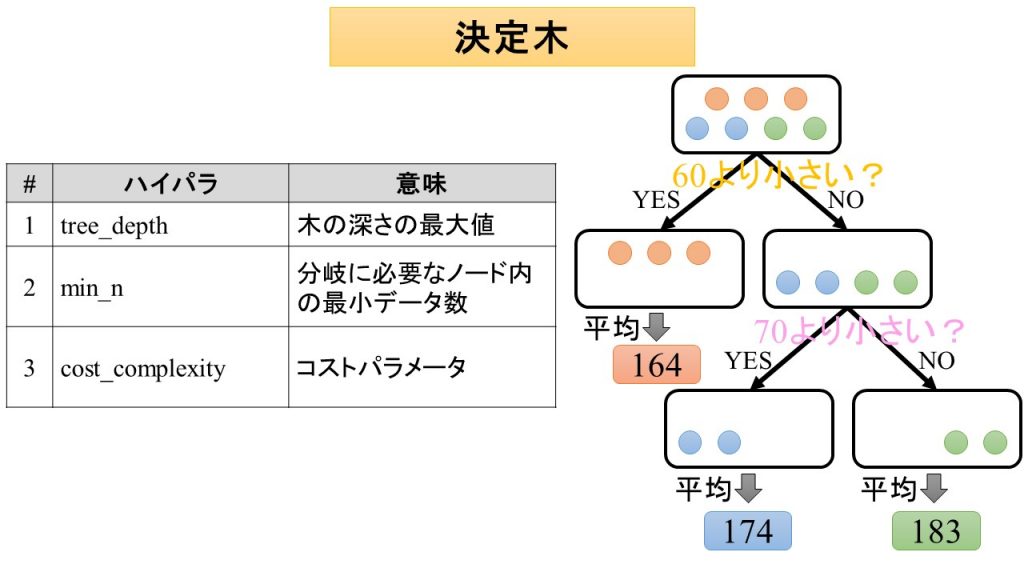
②ランダムフォレスト

全部で３つのハイパラがあります．

③勾配ブースティング

全部で8つのハイパラがあります．

アーリーストッピングってなんですか？？

アーリーストッピングは，学習をベストなタイミングで打ち切るための基準値を示しているよ！
木を増やして学習すればするほど，analysisに対する誤差は小さくなっていくけど，assessmentに対する誤差はあるところを基準に大きくなっていってしまうんだ．
このあるところ以上学習しても，過学習してしまうだけだからそうなったら打ち切る必要があるんだね！

イメージとしてはこんな感じです．

学習を進めるとこんな感じでanalysisの誤差はどんどん下がりますが，assessmentの誤差は逆にあるところを境に上がりはじめます．

我々の目的は評価データの誤差を少なくすることですから，評価データの模倣データであるassessmentの誤差が小さくなるように学習しなければなりません．

なので，assessmentの誤差が上がり始めたらそこで学習を止める必要があるのです．

実際はこの図のようにきれいになるとは限りません．

そこでstop_iterというハイパーパラメータで，ここで指定した数値の分だけ連続でassessmentの誤差が小さくならないようであればもう改善しないと判断し，学習を打ち切るのです．

実は，treesはハイパーパラメータをサーチする必要はありません．
木の数が多いときの精度を確認する過程で木の数が少ないときの精度も確認できるからです．
なので，treesを十分大きくして，それをstop_iterで制御するという方法が一般的です．

１．２．linear系

①線形回帰

全部で２つのハイパラがあります．

penaltyが正則化項の大きさを調整する係数，mixureがL1（Lasso）とL2（Ridge）の比率を表しています．

損失関数を最小にするように回帰係数（重み）であるWiを調整するというわけですね！

mixtureが1のとき，L1（Lasso）モデル，mixtureが0のとき，L2（Ridge）モデルとなります．

L1（Lasso）とかL2（Ridge）とか損失関数の数式は今はわからなくてOKです．

②ニューラルネットワーク

全部で５つのハイパラがあります．

ドロップアウトとエポック数ってなんですか？

ドロップアウト：重み更新時に中間層の一部のユニットをランダムに無効化すること
エポック数：学習の繰り返し回数のこと
を表しているよ！！

ドロップアウトをすることで重み更新のたびにネットワーク形状も変わるため，より学習の性能が上がります．

また，エポック数は勾配ブースティングの木の本数（trees）と同じような役割です．

エポック数も数が大きすぎると過学習してしまうので，その前に打ち切る必要があります．

勾配ブースティングのtreesと同様にepochsも理論上はハイパラチューニングをする必要はありません．
しかし，ニューラルネットワークは中間層が1層でそこまで計算コストが高くないため，tidymodelsではアーリーストッピングが実装されていません．
なので現状は，tidymodelsを使用する際は，epochsについては，アーリーストッピングを使用しないで普通にハイパラチューニングをしましょう．